|
The May 1934 issue of Flying
Aces magazine contained another installment in the "Principles of Model Building"
series it ran for many months. This particular article introduces formulas for calculating
the area of various shapes ranging from a simple rectangle to circles, parallelograms,
triangles, trapezoids, and more. It also demonstrated how to break irregular shapes
into individual constituent shapes, calculate the areas of each, and then add (or
subtract) them for a total area. It is a relatively simple procedure for anyone
familiar with basic geometry, but many modelers are not inclined toward the technical
side of the physics and mathematics which define govern flight. Calculation of area
is necessary for determining wing loading, control surface are ratios, volume (a
bit more complicated, but easily an extension of area calculation in three dimensions),
etc. As a side note, while preparing the sketches for posting here, I saw in Fig. 36
the definition of pi (π) and due to
the low original printing quality, the decimal point was barely visible so it appeared
to be at most a tiny random dot. The "1" is slanted so it looked like a division
line, so at first I though the author was giving
π = 3 /
4 as a fractional estimate of pi, which of course at 0.75 is way off of the standard
estimate of 3.14. I therefore inserted a prominent decimal point so the 3.14 would
be obvious. BTW, a common fractional estimate for pi is 22 / 7 = 3.145, which is
only 0.001264 away from the actual value of
π to six
decimal places (a mere 0.0402% error).
Principles of Model Building
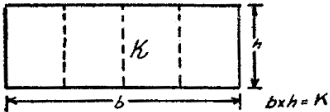
Fig. 35 -

Fig. 36 -
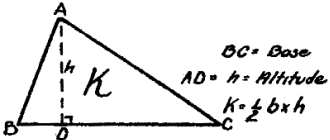
Fig. 37 -

Fig. 38 -

Fig. 39 -
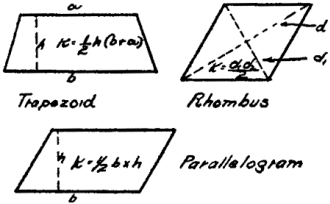
Fig. 40 -
By Avrum Zier
How to calculate the area of the various types of wings used on today's models
is a question that often puzzles model builders. This month Avrurn Zier applies
a few simple rules of geometry to help you with this problem. Just apply them -
and your troubles will vanish!
In the last Flying Aces we discussed the relative proportions of the surfaces
and briefly outlined the method of calculating the necessary area for any given
model. The moment arm, we said, was the distance extending from the center of gravity
to the fin, and it is this distance that determines the relative area between the
wing and the rudder. If the moment arm is long, less area is required, whereas the
converse is true when the moment arm is short. This month we discuss a very important
part of model designing - calculation of areas.
To many model builders the calculation of surfaces seems to become a troublesome
matter when wings such as the type used on the Springfield racer are concerned.
In this type of wing, we have to consider the curvature of the leading and trailing
edges before we can obtain the area to the nearest possible fraction. The curvature
on this wing makes it hard to work with; therefore, if we can possibly eliminate
the curves, the task would be much simplified. We are going to apply geometry that
will give the area of any wing when properly applied, and we will see just how the
area of the Springfield Racer wing may be found by simple application of formulas.
In Fig. 35 we have a perfectly straight wing, commonly called a rectangular wing.
Since it is the simplest, every model builder probably knows how to obtain the area.
General formula: B x A = K
The next type of wing is the rectangular wing with semicircular wing tips. This
type of wing involves the application of the area of a circle which is: 3.14 X radius
squared. Since the tip is a semicircle, we can obtain the complete area of the circle
and divide by 2. Adding this to the area of the rectangular wing, we have the complete
area of the wing. This, however, is a simple application, and merely serves to give
the fundamental basis of wing calculations. (Fig. 36.)
With the inauguration of irregular-shaped wings today, the process of obtaining
the area becomes difficult to master. First let us get familiar with the areas of
some of the common geometric figures, such as the triangle, circle, trapezoid, rhombus,
parallelogram, rectangle, and square. The most familiar figure is the triangle,
and it is also the most used figure. In Fig. 37 is shown triangle ABC with an altitude
AD. An altitude is a line drawn from any vertex perpendicular to the opposite side.
The side upon which the altitude falls is called the base, and the area of the triangle
ABC is 1/2 base x altitude.
With the formula of the area of the triangle fixed in our minds, we can proceed
to calculate the area of the wing shown in Fig. 38. When finding the area of any
surface, lines may be projected, providing the area contained within these lines
is subtracted from the total area of the figure. It is often useful to extend lines
so as to form a common figure such as the triangle.
The following example will show the value of producing lines. In Fig. 38 we have
the commonly shaped wings used mostly on contest models. By producing the leading
and trailing edge of the wing, we will have formed a triangle. Dropping a perpendicular
from the vertical C to side AB, we will have drawn our altitude. By the use of the
formula for the area of a triangle, we can obtain the area of ABC. Since ABC is
the portion we want, we find the area of the small triangle and subtract it from
the large triangle.
General formula is 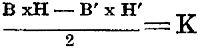
B equals base of large triangle: B' equals base of small triangle. H equals altitude
of large triangle. H' equals altitude of small triangle.
So far we have been considering the application of the triangle when finding
the area of wings having straight sides. We come now to the curved surfaces, such
as the rudder and wing tips. In cases where curves are considered, it is very hard
to obtain the exact area. We therefore try to obtain the result to the nearest fraction.
In Fig. 39 we have a wing similar in shape to the gull wing. The method of calculating
the area of this wing is as follows: Draw a rectangle around the wing as shown,
and draw as many tangents as possible. (Tangents are lines touching the curve at
one point only.) By doing this, you will have formed numerous little triangles whose
areas are found and subtracted from the area of the rectangle. The resulting number
will be the area of the wing.
The main idea when you are finding areas is to divide the area you wish to find
into as many geometric figures as possible, and then find the areas which, when
added, give you the completed area of the surface.
In Fig. 40 there are a few diagrams of commonly used geometric figures whose
areas are found by the accompanying formulas.
Posted June 18, 2022
|