|
Mr. Richard Von Berg wrote this great introduction to the
basics of shear forces within an airplane wing. It appeared in a 1957 issue of American Modeler, but
the principles have not changed since then. If you are familiar with the terms wing loading, shear,
compression, tension, and bending moment but are not quite sure exactly what they mean, this short piece
is exactly what you need.
Sheer Nonsense? No, Sir!
says Richard M. Von Berg and he tells you what every modeler should know about stresses that affect
your model in flight ...
What is shear, and why should you care two drops of glue about it? If you have never had a wing fold
on you, or have never cared if a wing did break, or have never wondered how to lighten a model for real
performance without sacrificing strength ... this is not for you.
Everyone knows that when his model is flying, the top section of the wing is in compression and the
lower section in tension, much as a floor beam at home. Did you know that this is always accompanied
by shear?

Fig. 1 - Shear force in a spar.

Fig. 2 - Wing loading, shear, and bending moment graphs.
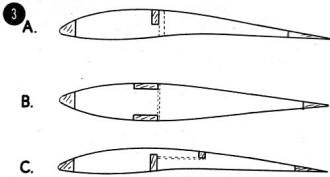
Fig. 3 - Shear webbing for various construction types.
Fig. 1 shows two thin pieces of wood of equal length in a bent position. Notice how the ends align
themselves. On the common surfaces of the wood, the top piece has slid along the bottom piece as shown
by the small arrows. Now consider if these two pieces were one piece and in the same bent position.
The sliding action could not have occurred, but instead we would have set up shearing forces within
the piece of wood trying to make the top and bottom halves slide just like the two separate pieces did.
This internal force on the wood is called shear.
Is this internal force worth talking about? If you have ever inspected the debris of a folded wing,
have you ever noticed split ribs? If you have, brother, that was too much shear. The author once won
a stunting contest, not because he was the best stunter, but because the contestant then leading in
points pulled out of a vertical dive into a gust of wind and his wing went into splinters from shear.
The sheer irony of it!
Fortunately, our engineers have discovered how this force is distributed within a wing. Fig. 2-A
shows the front view of a 40" span wing with a load of 80 oz. This could represent a 20 oz model in
a 4 G bump or a 10 oz model in an 8 G bump. Notice the small arrows, representing lift at 2 oz per inch,
equal the load of 80 oz. Fig. 2-B shows the distribution of the shear force within this wing.
At the wing's center the shear force is 40 ounces. If there is a center spar in this wing, the adjacent
fibers are trying to move in opposite directions with a force of 40 oz or 2 1/2 lb.! Balsa wood is very
weak in shear, as it is a soft-grained wood and the grain in most wing sections is in the direction
of the shear. We will later discuss methods of stronger construction for shear forces.
Fig. 2-C shows the distribution of the Bending Moment of a wing. This is expressed in inch-ounces
and at the center is 400 inch-ounces. This means, if the wing is 1" thick, the top wood has 400 oz of
compression force on it, and the bottom fabric has 400 oz of tension. Four hundred oz is 25 lb.! Wood,
however, is quite strong in compression. You can stand on a solid piece of balsa and not damage it.
Doped paper or fabric is very strong in tension and there is quite an area of it to take this force.
This great tension force illustrates why some heavier models are double-covered or covered with silk
or nylon. It is obvious now, however, that this is necessary only in the center third of the wing.
The curve of Fig. 2C shows clearly why wood covering is often used, or plywood dihedral joints, on
wing center sections. This curve also reveals the majority of model wings are overbuilt on two-thirds
of the wing or underbuilt in the center third. It is interesting to note that at the mid-point, or 1/2"
into the wing, there is neither compression nor tension, only shear.

Fig. 3 - Shear webbing for various construction types.
Fig. 3 shows typical wing sections of the usual rib and spar design. Fig. 3-A is a typical free-fight
wing. This wing section is somewhat weak for downdrafts and rough weather since it has no bottom spar.
To correct for shear forces the center ribs should have small strips of balsa in a vertical plane glued
to each side of the ribs as shown by the dotted line. Out further from the center only one strip per
rib is needed, until the outer third ribs have no strips.
Fig. 3-B is a typical stunt wing. A good method of correcting for shear is to use sheet balsa glued
between the spars as shown by the dotted line with the grain in the short direction (vertical). Keeping
the curve of III-B in mind., the center sections between ribs should be heavier balsa than the next
outer sections. The outer third of the wing needs none at all.
Fig. 3-C shows a wing section which is especially poor for shear, as the ribs have a tendency to
split from one spar to the other. Thin sheet can be glued, as shown dotted, between the spars, much
as described above with the grain in the short direction.
That's pretty much the story of shear as applied to model wings. It isn't so complicated, is it?
By keeping these things in mind on your next model, you, too, can watch your wings stay together with
complete confidence.
References: Steel Construction Manual of the American Institute of Steel Construction; beam diagrams.
Physics, Hausmann and Slack; elasticity.
Posted November 26, 2016
|


