How to Build Better Wings
July 1962 American Modeler

July 1962 American Modeler Table of Contents Aeromodeling has seen significant changes over the decades both in technology and preferences. Magazines like American Aircraft Modeler, American Modeler, and Air Trails were the best venues for capturing snapshots of the status quo of the day. All copyrights are hereby acknowledged.

Hal deBolt was a well known and respected model aircraft designer in the early days of radio control. By 1962, when this "How to Build Better Wings" article appeared in American Modeler magazine, there were some proportional radio systems coming on the market, but a lot of fliers still used escapement, galloping ghost, or reed systems. With somewhat limited control , having an airplane that was inherently stable or neutrally stable was important for success. Negative stability usually meant disaster. One way to minimize airframe related issues is to build on a well-designed jig - especially for the wing and tail surfaces. Even today's laser cut, perfect fitting kit parts are of no use in obtaining a true airframe if the surface they are built on is twisted or bowed. This article offers a simple jig that can be used for building any normal wing. If you are one of the rare builders left and are having problems with trimming your model to fly predictably, try checking the trueness of your current models, and then consider building your next project on a jig. 

How to Build Better Wings

By Hal deBolt

May I tell you a little story? Several years ago I was testing a new model of different design and came up with a perplexing problem. This plane just did not seem to have any directional stability; one time it would want to drift to the left and the next it would be going to the right. All sorts of adjustments were tried to make it fly straight but none had the least effect. In fact, it had me pretty well stumped.

A complete and thorough check was made of the entire model, everything seemed in order except the wing. The wing had been built without jigs and when a careful check was made of it several small warps showed up. From what could be determined these warps should have been cancelling each other out, or at least a definite drift condition should have been created instead of the "wandering" problem that was present. We agree that directional stability can be disturbed by wing warps, but it is also true that other phases of the model design can also cause it.

Some chap asked me how I could pin the trouble down to one thing unless I had an absolutely true model to start with. I decided that from then on I would be certain that I had true wings and to be positive of this I would build all my wings in jigs. Before this I had always hesitated when it came to the idea of a wing jig because I figured it was an awful lot of work and some expense. Now, I can say that the expense is less than the cost of one warped wing and the time is made up manyfold by the ease of assembling a wing in a good jig!

Today's R/C models are flying faster and faster and we are asking them to perform many intricate maneuvers. High top speeds plus normal low speeds means a great flying speed differential with our models.

Warps do not like these conditions at all. We can adjust for the effect of a warp at a given air speed, but it is almost impossible to do it for all flight speeds. The same goes for a warp in maneuvers, you can compensate for the warp when doing inside loops but when you perform an outside the problem is accentuated by the adjustment you made to help the insides! The only real answer is to have true wings.

Then, too, a warp detracts from the efficiency of our model. The warp itself creates drag; when we compensate for it with an adjustment we have doubled the original drag. So you are sold on the idea of wing jigs? Let's see what is required to build one and just what kind would fit our needs.

Generally speaking there is one type of wing construction today, it uses the so-called D-Section" leading edge spar and usually a trailing edge spar, too. This type, when it has a straight chord, lends itself readily to a universal sort of a jig in which wings of many sizes can be built.

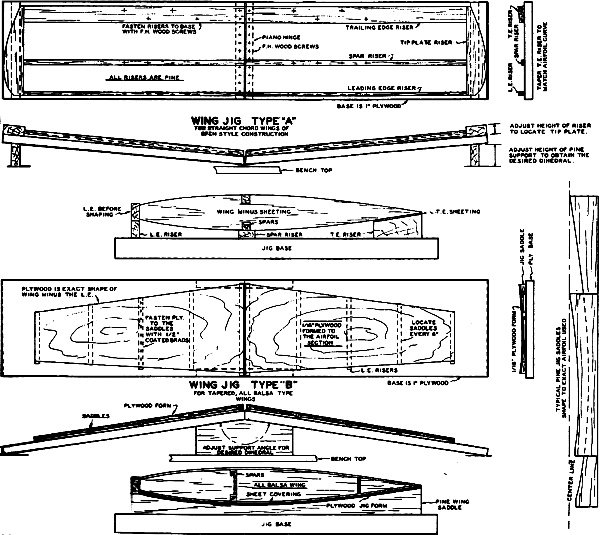
The drawing shows a Style "A" jig, this is the universal one and easiest to construct. We purposely did not give exact dimensions because they will vary according to the type airfoil used and the size of the wings which you generally build. The only item of importance is to choose a base board of straight 1" plywood and a size slightly larger than the biggest wing you expect to make .

The gimmick behind this jig are "risers" which can be varied in size and location. For example, let's set up the jig for a 12" chord wing. First you make a template of the airfoil to be used. Trace this on paper and locate the leading edge, spars and trailing edge sheeting. Draw a line tangent to the bottom of the spar and parallel to the center line of the rib. This will be the base line and represent the top of the jig base. Add the trailing edge sheeting exact size. If you drop lines directly down to the base line from the leading edge sides, spar sides and trailing edge sheet sides you will have the exact size of the "risers" needed for your jig. These should be cut on a circular saw from . straight white pine. When finished fasten them to the base board and after your jig is hinged, you are ready to begin building a wing.

Construction is started by placing the leading edge on its riser, the spar on its riser and also the bottom trailing edge sheeting. The ribs are cemented in place and the assembly work continued as far as possible before it is removed from the jig-this includes all dihedral braces.

If you will observe closely it can be seen that wings of various chord sizes and airfoils can be turned out simply by changing the location of the risers or their sizes.

Another type of wing is coming into prominence because of its efficiency and I suppose its better looks. This is the completely tapered wing using all-balsa construction. These, difficult to build, are practically impossible to construct true without a jig. The jig labeled "B" was developed to build this type. When I say developed I mean it literally; our group experimented for a long time before we found this to be the only practical way to build a jig for this wing type. In the end it also proved to be the easiest.

Idea behind this is that you actually form the wing in the jig which is built to match the exact outside contour of the completed wing. The fact that the jig is one piece of 1/16" plywood means that when this is pulled down into the airfoil saddles as shown it will naturally assume all the compound angles necessary for the actual wing's surface. This characteristic is the secret to the success of this compound taper wing jig.

The jig shown is also for a surface used on a low wing model. Note that in such case the wing is built inverted. By assembling the wing upside down it is possible to complete it before removal from the fixture. If it was built upright it would be extremely difficult to install the landing gear mounting.

With Type "B" jig we also utilize 1" plywood for the base, only this time we do not hinge it at the center. Instead, a pine support is cut to the dihedral angle desired. By changing the angle on this support wings of varying dihedral can be built.

The true outline of your wing is laid out on 1/16" plywood, this is carefully cut out. Wing outline is also drawn on the jig base in its exact location. Since this is a compound tapered wing it is necessary to layout each rib separately. Then these ribs can be used as templates to make the jig saddles. A saddle is required about every 6 inches along the span so a rib is selected whose station falls close to each. The saddles are from pine strips 1/2" thick, width is 1/4" more than half the thickness of the center rib. A saddle is cut to length for each station on the jig - center, middle and end saddles are made longer to act as risers for the wing leading edge. On the two center saddles scribe a center line which 1/4" higher from the bottom of the saddle than 1/2 the thickness of the rib. Example: If the rib is 1-1/2" thick, one half of this would be 3/4". So add 1/4" to this for clearance and the center line of the saddle would be 1" from the bottom edge.

Now that the height of the center line has been determined a center line of the same height can be drawn on each of the saddles. Next the shape of each corresponding rib can be drawn on the saddles using the center lines laid out for the purpose. These shapes are cut into the saddles and carefully finished to size. The saddles are now fastened to the base board and the plywood nailed to them. To fasten the plywood down you line it up with the saddles and nail it down the center with one brad in each saddle.

Then you work from the center out to the edges nailing as you go, this will assure that the plywood forms exactly to the saddles and thus the true shape of the wing.

To build this all-balsa wing you first glue up some 2" wide sheets on a flat surface until you have a width greater than the maximum chord. It is important to use 2" as the glue seams act as strengtheners for the skin spanwise. After these have thoroughly dried they can be cut to the outline shape of the wing panels. They are sanded well with a sanding block until the surface is smooth. Now the two skins are put into the jig and located correctly by fitting the center line joint. Once fitted the center seam is cemented and the skins are pinned to the plywood surface. The top spar is cemented in place. This is followed by the ribs and lower spar.

At this point the wing construction is well along and can be completed in an orderly manner. When everything is in place and the aileron linkages installed you are ready for the bottom covering. This is put on a piece at a time instead of a whole skin as was done for the top. After the bottom skin sheets are installed it is wise to leave the structure in the jig for at least 24 hours to assure that all internal cement joints have dried. You now have a wing which is true; it is completed by final sanding and covering.

These jigs can be used over and over again and more than one builder can take advantage of them. This makes them a very desirable club project, something everyone can lend a hand in preparing.

For the R/C flyer who has a brand new expensive multi-channel model ready for its first test hop it sure is reassuring to know that he has a true wing on it.

Harold deBolt's Wing Building Jig

Posted May 15, 2024
(updated from original post on 6/21/2014)